from orbits to external effects

Understanding Physical Uncertainty and Complementarity

By Marlon Hoffmann

The year is 1925 and a 23-year young Werner Heisenberg, pained by his hay fever, is spending the summer months on Heligoland, far away from anything that might distract him, thinking about the inner workings of the atom. What exactly was he thinking during those days? What was the great insight that would shake the foundations of physics to this day? While we cannot exactly look inside the head of anyone long dead, based on his writings and the discussions following afterwards we can certainly try to reconstruct the main threads of argumentation that might have been at play and though this might not exactly be how Heisenberg would have approached the topic himself (in fact it most certainly is not), we can get a feeling for how we might have discovered something this profound ourselves.

But first we have to go back to over a decade beforehand, when atomic theory has just begun to really take hold within the physics community. What was known back then, was that atoms are themselves composed of two types of smaller particles: heavy, positively charged protons and much lighter, negatively charged electrons. (For most elements, there are also electrically neutral particles called neutrons inside the atom’s nucleus, but we will ignore them for now.) The simplest case would be then that one has one electron and one proton making up an atom of Hydrogen. From classical electricity one knows that opposite charges attract, so the electron would be pulled towards the proton, while the much heavier proton stays virtually unaffected. This cannot be a stable configuration, unless one imparts some initial movement on the electron that causes it to revolve around the proton, like planets orbiting the sun, or a satellite orbiting the earth, constantly falling towards the bigger mass, but also constantly missing it.

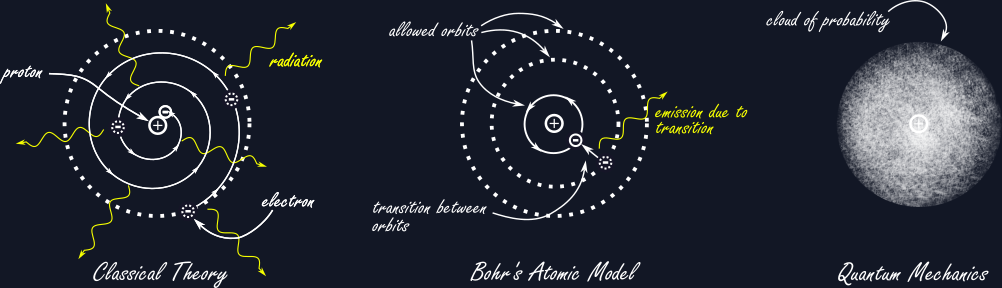
There is just one big catch and physicists back in the days were very aware of this: When viewing the electron orbiting the proton from the side, one would see a continuous oscillation of a negative charge around a positive one, like a charge running up and down an antenna and like an antenna this would emit radiation or light. This already is strange to think about, as we do not usually see matter glowing constantly on its own. But apart from disagreeing with daily observation, the radiation would carry away energy from the electron, causing it to slow down and eventually collapse into the proton. Atoms would destroy themselves only a tiny fraction of a second after being initially created. This is obviously not a good model of reality.

Being aware of this problem, Niels Bohr proposed a solution: He just postulated that there would be stable orbits that do not radiate. If this feels like a hack, then it’s because it is, but the assumptions went further than this. To agree with the observation that atoms do in fact glow with very specific frequencies when for example heated up, he postulated that electrons can change between those allowed orbits by absorbing or emitting radiation. The frequency or colour of the radiation is given by the change in energy of the electron during that transition between orbits. This theory works for the radiation spectrum of the Hydrogen atom but does not fit the data for any other element of the periodic table. Also, the assumptions are very ad hoc and it is not clear how to generalize this theory to other types of systems.

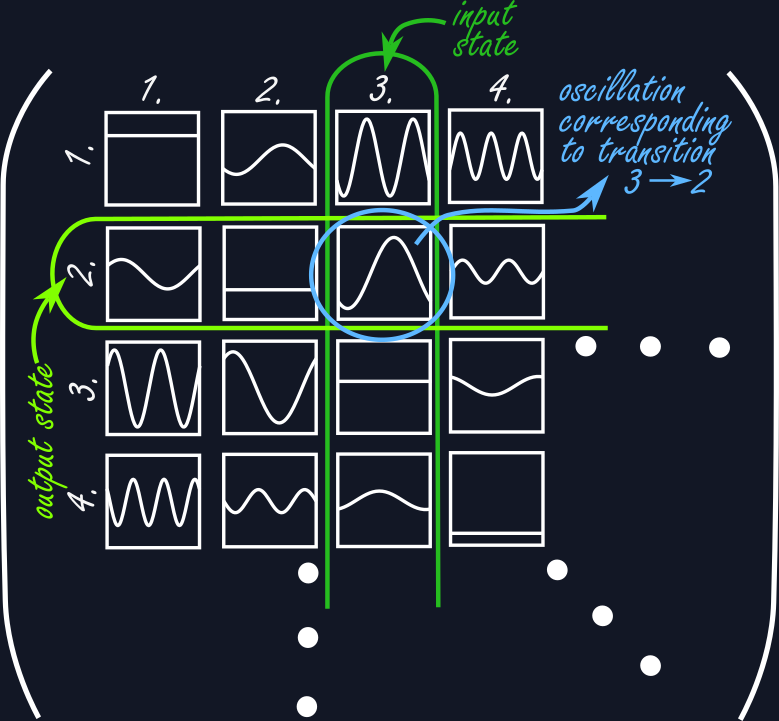
This is where we return to Heisenberg on Heligoland. How would he solve the issues of Bohr’s quantum theory? The idea is rather simple but surprisingly effective. Just do away with orbits and focus on what can be actually observed from the outside. The key insight for developing mechanical laws for the atom was that while stationary states do not radiate and thus cannot be based on oscillations of any kind, it is the transitions between states that are oscillatory in nature. In the end what can be seen from the atom is not the orbit of the electron but the light it radiates when it changes state. If we should focus on what can be observed, then the mathematics should keep track of every possible transition from one state into another. What has to result then is a sort of table, where the number of columns record the input state and the number of rows the output state and it is the entries of this table that exhibit the oscillations associated with those particular transitions. The number of possible states could be infinite, in fact most of the time it is, hence the table itself is infinite in size. In mathematics these tables are called matrices, but Heisenberg was not aware of this at that time.

We have saved the atom from self-collapse, but at what cost?

One could ask what a clearer physical picture could be, with all this up until now being rather abstract. In classical physics the thing that oscillated was the position of the electron, which was clearly defined. So where exactly is the electron in the context of matrix mechanics? It seems intuitive that at any point in time, it would be most likely close to the proton somewhere, but formulating observable quantities as these tables of multiple values, forces us to consider multiple answers to the question of where the electron is to partake in the physical reality at the same time. There is a sort of fundamental uncertainty here. Quantities like position and velocity, for example, cannot be determined with arbitrary precision, and this follows directly from the mathematical formulation.

At the same time, this uncertainty is what saves the atom from inevitable collapse, as the fundamental uncertainty in position prevents the electron from approaching the proton arbitrarily closely. In the end, Wolfgang Pauli was able through meticulous bookkeeping of the infinite number of matrix components to first obtain the precise energy spectra of the hydrogen atom systematically from the ground up. If it works, it works!

We have saved the atom from self-collapse, but at what cost? Turning theoretical physics on its head by introducing cumbersome matrices into the equations might be almost the most benign consequence of this, as will be seen. Soon after quantum mechanics using matrices has been thoroughly developed, Erwin Schrödinger provided a different formulation of quantum physics, where particles are described using waves in space, stationary states result as standing waves and the oscillatory nature of transitions becomes apparent as the shape of the wave function changes over time. Even though this is usually how quantum mechanics is first introduced to students, for it being more intuitive than abstract matrices that do not have a clear picture within the framework of classical physics, the two formulations are in fact mathematically equivalent, no one being fundamentally more powerful or insightful than the other.

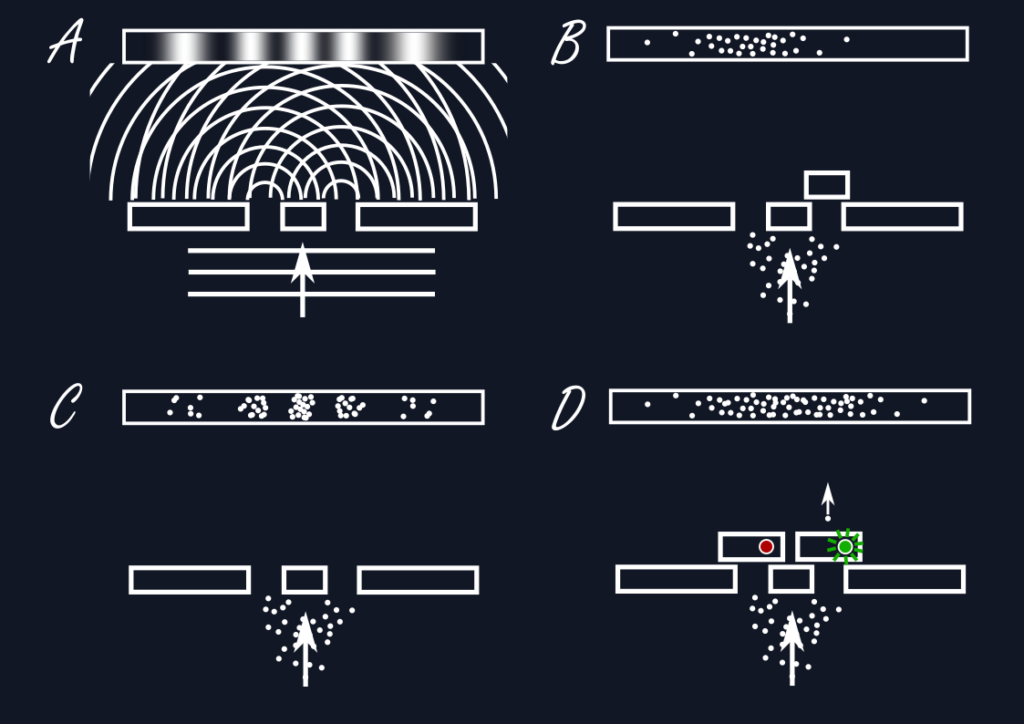
There are curious consequences that result from the wave formulation: When a wave passes through a wall with two small parallel slits cut into it, we can imagine the wave propagating through both slits at the same time, creating in effect two waves that can overlap and interfere with each other, forming a stripe pattern of waves amplifying each other and cancelling each other out. But what happens when this is applied to a single electron? Where does it end up after the slits?

If we were to measure the position of the electron behind the double-slit then all that can happen is for us to observe a single value for the position and not a stripe pattern, no interference. If we were to repeat this experiment many times and take a record of where the electrons end up, only then one would see a stripe pattern of places where many electrons end up and where there are only few to none. This presents us with an interesting conundrum: The individual electrons must have known where they can end up and where not, i.e., they must have known about the two slits the entire time. If the experiment is done again with one of the slits blocked, then the interference pattern disappears. Could a single electron have passed through both slits at the same time? One could get the idea to just measure and record the slit the electron passes through as it does so. But then again, the interference disappears and one only sees the electron passing through one of the slits at random, as one would expect for a single particle.

Just do away with orbits.

Thus, one cannot have it both ways: Either one can see wavelike interference behind the double slit or one can learn something about the path the particle actually takes and which slit it goes through, never both. The correct physical description in a particular situation appears to depend on the context determined through the eventual act of measurement. Neither can be complete in describing the underlying physical reality, while at the same time being fundamentally in conflict with each other. This is what Bohr has termed complementarity.

It seems as if the original mistake was again the assumption that there is such a thing as a definite trajectory the electron takes, i.e., a definite slit it must have gone through, of which we can find out something through measuring the position the particle is at along the way. But in fact, trying to pin down the intermediate behaviour through measurement affects the state of the system in a rather destructive way. Observation forces a particular outcome to arise, whereas the correct description of the particles’ evolution prior to measurement must include many different possible outcomes, each with certain probabilities. It is when trying to find deeper meanings and interpretation of these mathematical descriptions in “plain language” that the conceptual difficulties arise.

Of course, the same rules that govern the strange world of quantum particles need not apply to larger objects or even us humans. Simultaneously, everything we know and interact with on a daily basis is made up from those particles so a sharp distinction between the quantum world and the human world does not seem obvious either. In that sense any quantum weirdness seems to be washed out on these larger scales that we are used to by the messiness in between.

Fundamental uncertainties are mostly limited to the quantum realm and do not usually extend to anything bigger than a molecule, though these limits can be and have been pushed severely in the lab. Nonetheless, there are uncertainties and complementarities we have to deal with on a daily basis. The rules that govern human experiences, however, are more rooted in psychology, human interaction and societal norms that are not as hard and fast as the mathematics of matrices and wave functions.

So, if we were to ask ourselves, what might have pushed Heisenberg to that infamous encounter with Bohr in 1941, what they were discussing, what his motives were, then we shouldn’t hope for conclusive answers through simple, one-dimensional observation. If we are to limit our judgement to the external effects that these people had on their surroundings and the world at large, then we must consider the fundamental uncertainties and apparent contradictions that go with them and need to take multiple different viewpoints into account. In a sense, mathematics does become strange when applied to people.